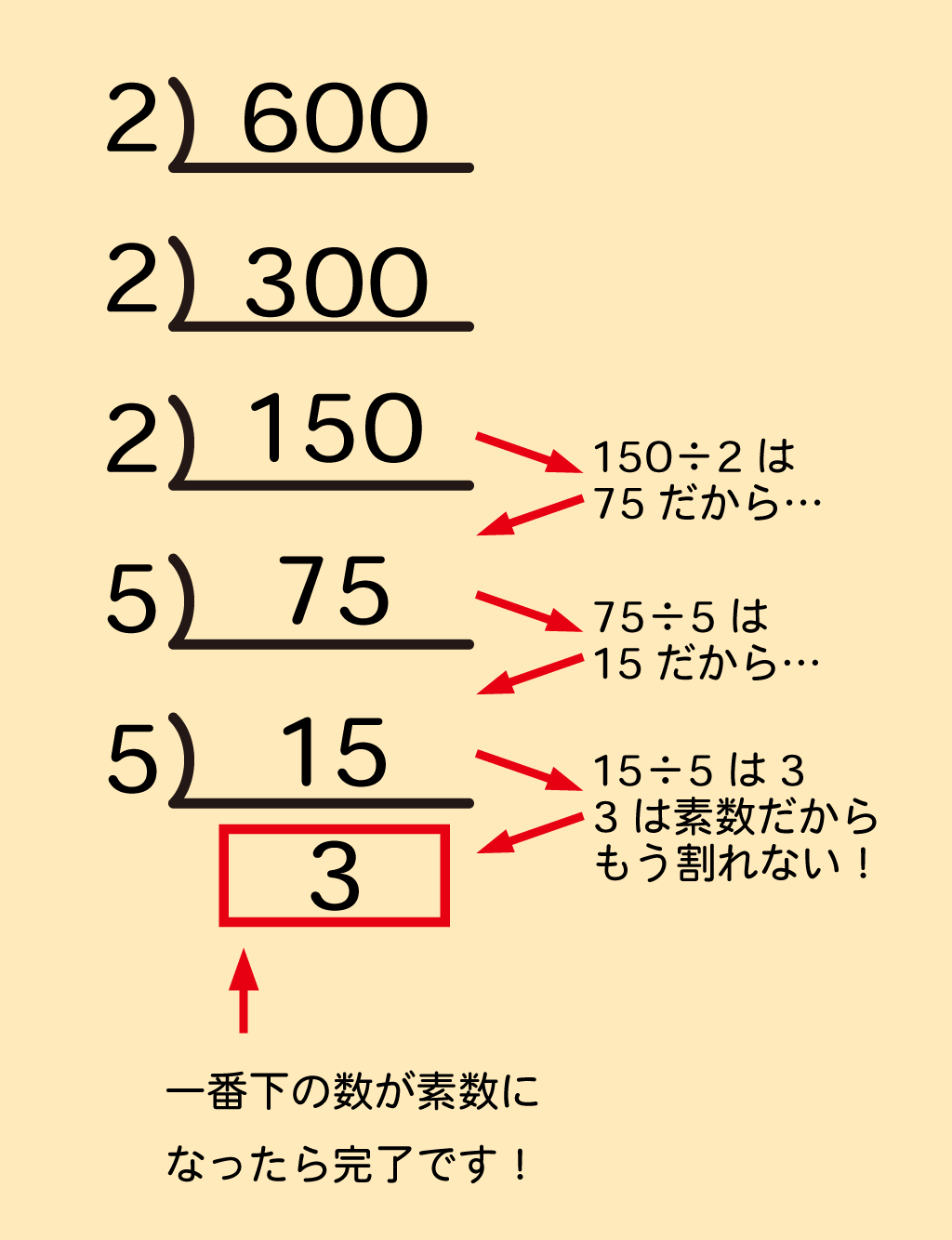
25 ++ 5 の 平方根 306108

 4 の平方根 ＝2 5 の平方根 ＝ 6 の平方根 ＝ の平方根はそのうえの数字の「521」だよ。 やったね。 13ステップは長すぎるぜ^^ まとめ：筆算をつかった平方根の求め方は辛い 平方根の求め方に筆算をつかうと、 でかい数の平方根を求めるとき;5の平方根 ⇒ \(\pm \sqrt{5}\) こんな感じで平方根を表すことができるようになるんだ！ ただし、4の平方根のように\(\pm 2\)と数が見つかる場合には

ルート2 ルート3 ルート5の覚え方など 高校数学の美しい物語

5 の 平方根

5 の 平方根-本题要求编写程序，计算平方根序列 的前N项之和。 可包含头文件mathh，并调用sqrt函数求平方根。 输入格式 输入在一行中给出一个正整数N。 输出格式 在一行中按照"sum = S"的格式输出部分和的值S，精确到小数点后两位。 平方根って何なの？ まず最初に、平方根という聞いたこともない単語。 平方根とはある数字のことなんですが、 カンタンに言うと、2乗（同じ数を2回かける）したらできる数字のことです。 たとえば、2は4の平方根になります。 3は9の平方根になります。 4は16の平方根になります。

開平方 平方根の求め方 時じくの香の木の実

「平方根」というのは2つあります。 たとえば、 ・9の平方根は？ と聞かれた場合、 ・2乗すると9になる数は？ という意味なので、 「＋3と、－3」 の 2つの答えがあります。 （ここまではもう大丈夫ですね！） 同じことを根号（ルート）で表せば、平方根のかけ算と割り算は、 ルートの中身をそのままかけ算・割り算します。 \(5\sqrt{2}×3\sqrt{2}\) を計算してください \(5\sqrt{2}×3\sqrt{2}=(5×3)\sqrt{2×2}\) まず、わかりやすい例として 25 の平方根 (√25)を求める方法から。 計算手順の基本は、「奇数を順次引いていく」だけです。 これだけで平方根が求まります。 この場合、5回で計算が終了するので、√25 = 5 です。 このことの数学的な意味を、図形で検証

5 ≒ \sqrt{5}\fallingdotseq 5 ≒ （富士山麓オウム鳴く） これもわりと秀逸です。 ぜひ覚えましょう。9の平方根は、3と－3 このように答えればOKです。 （まとめて と答えてもOKです。） なお、同じように考えれば、 16の平方根は、±4 25の平方根は、±5 とすぐ答えることができます。 「平方根は、いつも2つある」 ことを、 忘れないでくださいね！ 「2乗にこれらの平方根を，記号 を使って次のように表す。 正のほうを a，負のほうを－ 0の平方根は0だから， 0＝0である。 を使って平方根を表す 5の平方根を，根号を使って表しなさい。 正の数の平方根には，正の数と負の数の2つがある。

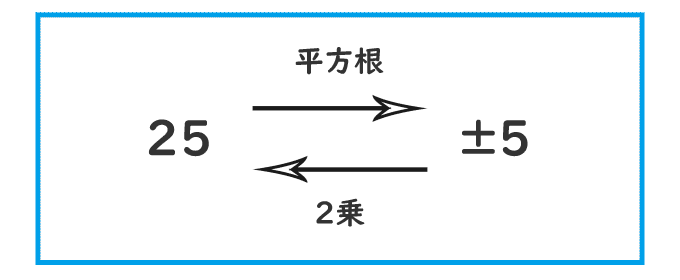
 5的算术平方根是：√5，因为5开平方根是个无限不循环小数(即无理数),所以只能写成√5。 扩展资料 平方根定义： 如果一个数的平方等于a，则这个数叫做a的平方根，如果x2=a，那么x叫做a的平方根，这里a是x的平方，它是一个非负数，即a≥0。 把5写在根号内，得数（平方根）写在根号上面。 2 的平方是4，最接近5，所以先"商"（其实不是商，是平方根）,5减4余1。 第二步，在1后面补两个0（每一步都补两个0），用100做被除数；第一次的平方根是2，2×=40； 100除以40多可以商2；就用42做除数，100除以平方根とは2乗の逆のこと 「5の2乗は25、また、 (−5)の2乗も25である。 」 そのため25の平方根は5と−5である。 5と5のことをあわせて±5と表記することもある。 例) 25の平方根は±5 平方根とは2乗の逆のことなので、 2乗したときにAになる数がAの平方根

中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ

中３数学 平方根２ 5 加減 展開 復刻版 Youtube

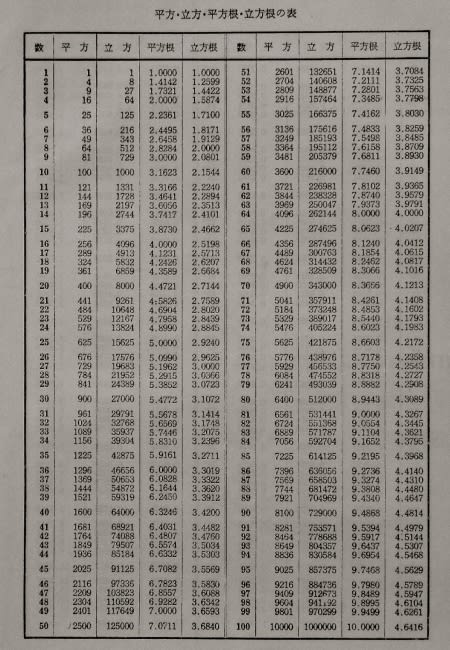
1001 rows オンラインの平方根計算機を使用して、入力した数値の平方根を見つけます。 平方根 数学では、数値xの平方根は、r 2 = xとなるような数値rです。 例えば、 1 5 2 = 25であるため、25の平方根は5です。 3 2の平方根はおよそです。 3 Piの平方根（π）は約です。 平方根テーブル 以下は、5桁に丸められた1〜1000の平方根テーブルです。株価の単位時間あたりのリターンの計算 アンケートにご協力頂き有り難うございました。 送信を完了しました。 平方根・累乗根 のアンケート記入欄 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60歳以上 職業 1辺が√5の正方形を作図すればよいのですから 三平方の定理より√(1^22^2)=√(14)=√5 なので 2マス×1マスの長方形の対角線の長さが √5になります。 あとは下図

中３数学 平方根 有理化 Youtube

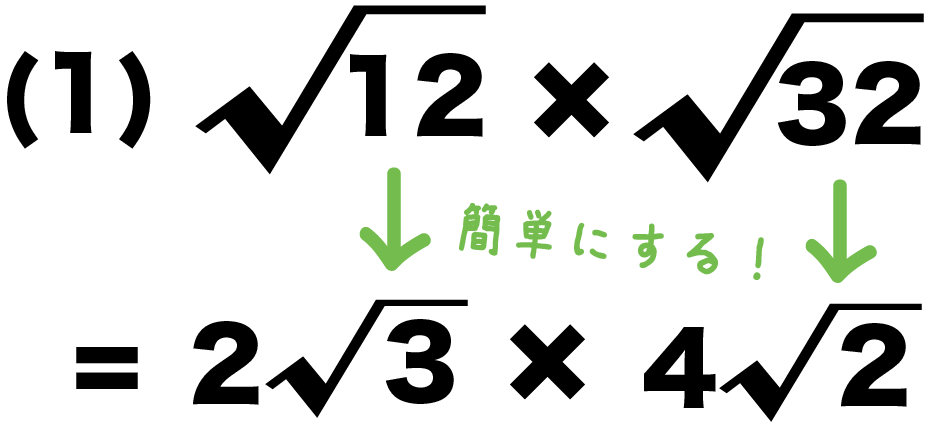
平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく

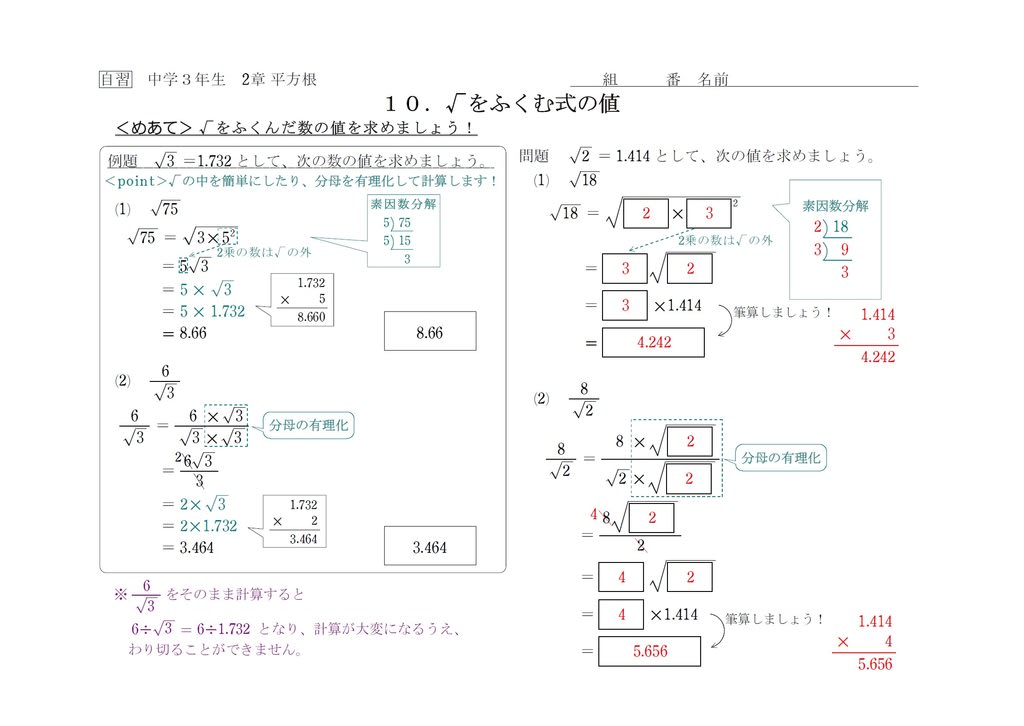
"平方" 通常是写成一个小小的 2： 意思是"4 的平方等于 16" （小的 2 代表数在乘法里出现了 2 次） 平方根 平方根 是平方的相反： 3 的平方是 9，所以 9 的平方根是 3 就是问：ルートとは？平方根の求め方を解説！分数や小数の場合はどうやる？ 平方根、ルートの値を語呂合わせ！覚え方まとめ←今回の記事 a√bの形に変形するやり方とは？ 平方根の大小関係を不等号で表す問題を解説！ 根号を含む式の値の求め方とは？2、5、81の平方根は？ 2、5、81の平方根を下記に示します。 ・2の平方根 ⇒ ±√2 ・5の平方根 ⇒ ±√5 ・81の平方根 ⇒ ±9 81を素因数分解すると「81＝3*3*3*3」です。ある数の2乗になるよう整理すると「3*3*3*3＝9*9（9の2乗）」ですね。2や5の平方根は下記も参考

平方根 ルート の足し算と引き算のやり方と計算問題 中学3年生数学 Irohabook

エクセルでルート 平方根 を表示 計算する方法 関数使用 Office Hack

平方根の覚え方 2、3、5などの平方根の値は暗記すると便利です。平方根の値は、物理学や工学で使うからです。語呂合わせを下記に示します。 上記の平方根は、最低限覚えるべきでしょう。 平方根の公式と問題 平方根の公式を下記に示します。 5の平方根 5の平方根の概要 ナビゲーションに移動検索に移動「√5」はこの項目へ転送されています。barbee boysのアルバムについては「√5 (アルバム)」をご覧ください。過去にグループ名が√5であった音楽グループについては つまり、5は25の平方根であると言えるのです。 なんとなくイメージが掴めたでしょうか？ 難しく考えないでも、 の平方根を求めなさいと言われたら、何を二乗すれば になるのか考えればいい ということです。

5 8 8分の5 の平方根を答えなさいという問題の答えは 5 8 ルート8分の Yahoo 知恵袋

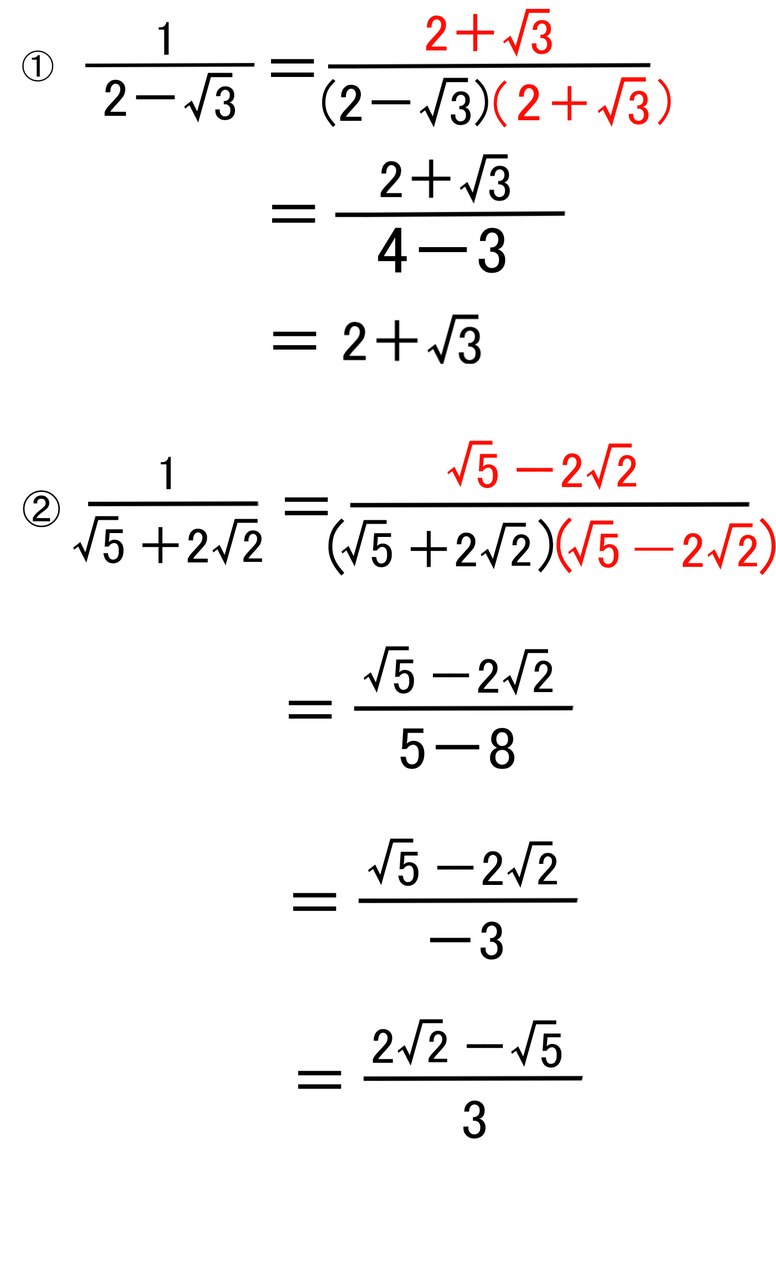
平方根 5 分母の有理化 バカでもわかる 中学数学

平方根や累乗根を数式で表す場合は、ルート（ ）という記号を使います。 9の平方根を表す場合は、 9 と書きます。 9の平方根は3なので「 9 =3 」となります。 累乗根を表す場合は、ルートの前に小さい数を置くことで何乗根かを表します。 – √3 × √5 が計算できそうだ。 平方根の掛け算では「√の中身」を計算してもよかったよね？？ だから、 – √3 × √5 = – √15 になるね。 あとは左の足し算。 2√2;

平方根 加減法 無料で使える中学学習プリント

Tossランド 平方根 の暗記プリント Dl可

平方根の加減の問題です 1 2 3の問題の解き方1つでもいいので教えてくださ Clearnote

平方根の大小関係と大小比較の練習問題 難易度別に解説 坂田先生のブログ

２乗 平方根

平方根の範囲です 教えてください 答えは 4 25個 5 9個 です Clearnote

平方根 応用 問題 平方根 問題 応用 Gasaktuntasm62p

中３自習 平方根７ 加減１ 中学数学の勉強に

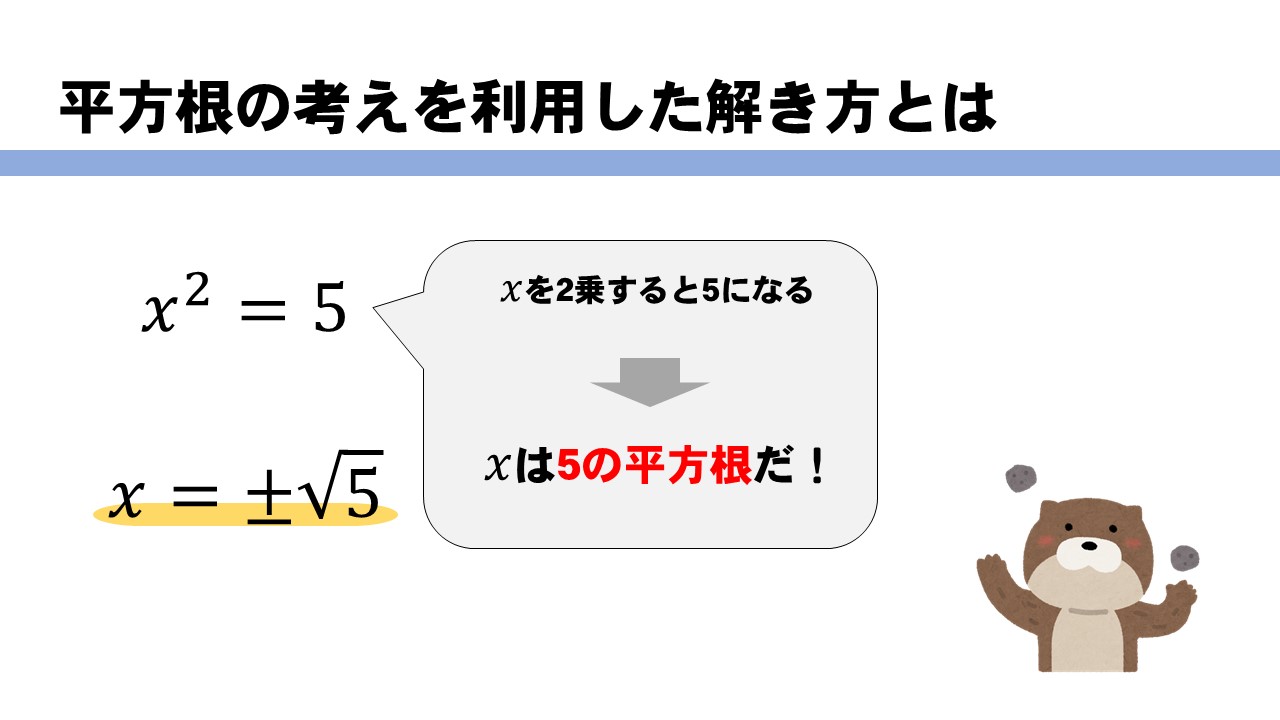
二次方程式 平方根の考え方を使った解き方はどうする イチから解説 中学数学 理科の学習まとめサイト

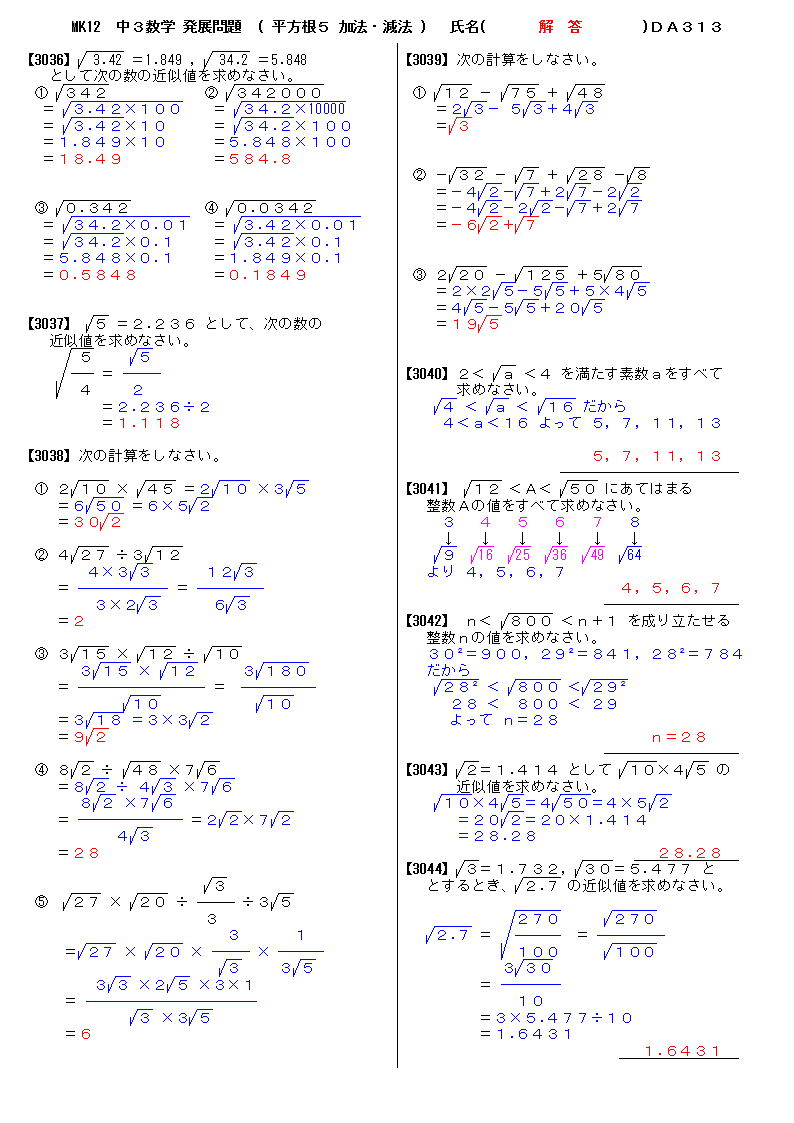
無料 中３数学 発展 応用問題 解答プリント 313 平方根５ 加法 減法

5の平方根 Wikipedia

平方根の問題が分からないので教えてください 5分のルート2 ルー Yahoo 知恵袋

1

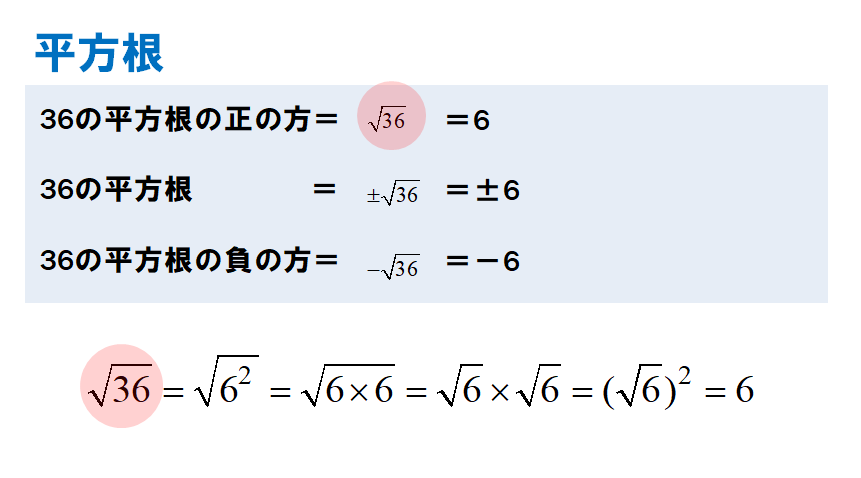
中3数学 平方根の性質の定期テスト対策問題 Examee

添削課題 数と式 平方根の計算 都立西高 灘高 追記5月21日解答 Matsu Math Note

超基本だけど入試にも出る 平方根の基礎問題 2日目 ベントー

平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ

3 26第２章平方根 根号の使い方 フロントエンドなブログ

中学の数学 平方根 を理解して受験を乗り切ろう 札幌市 学習塾 受験 チーム個別指導塾 大成会

にわか神道の愛燦々 富士山麓にオウム鳴く 5の平方根 の予言 三六屋からす一家 本 通販 Amazon

平方根no ５ 平方根の大小 Youtube

平方根の手計算による解法 タックの庭仕事 黄昏人生残日録

日本ケイデンス デザイン システムズ The Sound Of Cadence Online

平方根 ルート の足し算 引き算の仕方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

1 １ の は 5の平方根は 5 なのに なぜ2 の 2 Clearnote

5の平方根 Wikipedia

中学数学 平方根の利用 ママ塾ノート

3 29第２章平方根 整数にはさまれた平方根 フロントエンドなブログ

中学３年生 数学 平方根 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

５の平方根は ルート５ですか また ルートの中に５を入れると Yahoo 知恵袋

ルート2 ルート3 ルート5の覚え方など 高校数学の美しい物語

平方根 2 ルートと平方根の違い バカでもわかる 中学数学

Laf先生 平方根の大小 9と5はどっちが大きい 中3数学 平方根 Powered By Line

3 28第２章平方根 平方根の大小 しもじまの数学

ルート5 デザインtシャツ通販 Tシャツトリニティ

平方根 2乗するとaになる数 教遊者

機械式計算機による平方根の計算

平方根 4 の 1 の 2 平方根 5 の 1 4 の Clearnote

1

中３ 数学 平方根５ 有理数と無理数 ４分 Youtube

富士山麓オウム鳴く 以外のルート5の値の覚え方3選 Qikeru 学びを楽しくわかりやすく

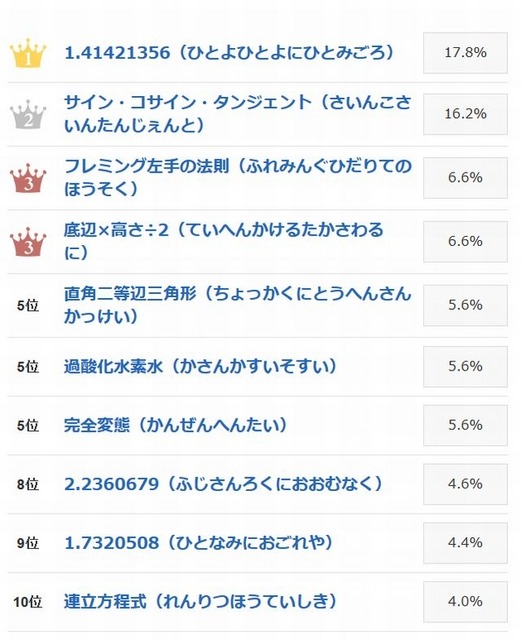
脳裏にこびりついた つい声に出して言いたくなる理数系の用語 たち レスポンス Response Jp

数学 中3 16 平方根 Youtube

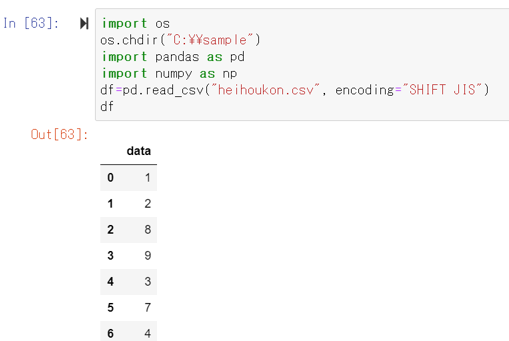
Python Pandasとnumpyにて平方根 ルート や立方根の計算を行う方法 列ごとに一括で ウルトラフリーダム

5の平方根 Wikipedia

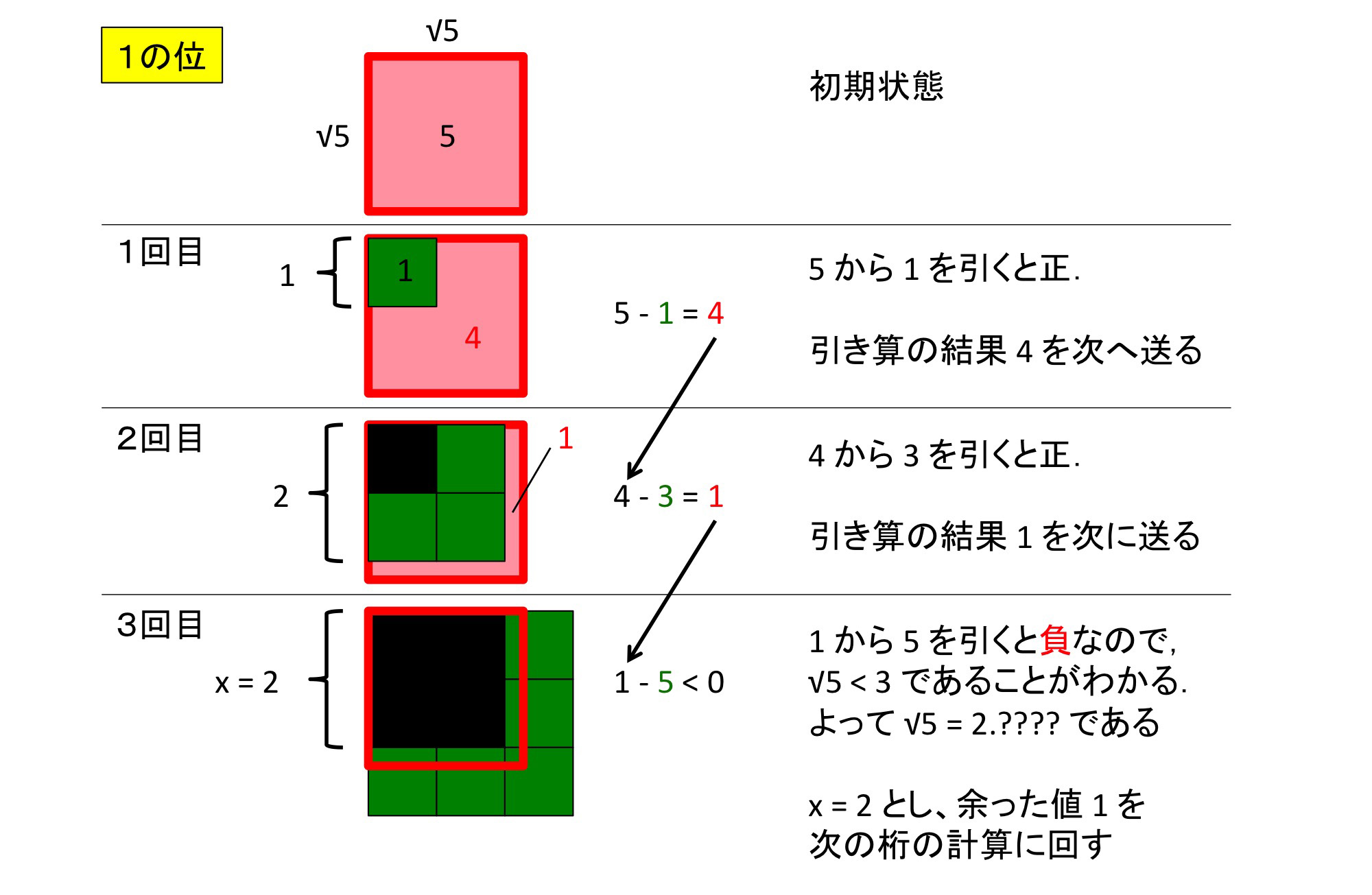
中３自習 平方根５ 近似値 中学数学の勉強に

平方根 ルート の足し算と引き算のやり方と計算問題 中学3年生数学 Irohabook

因数分解 おしゃれまとめの人気アイデア Pinterest 花梨 21 平方根 素因数分解 学び

2次方程式 平方根の考え方を利用した解法 その1 すうがくラボのブログ

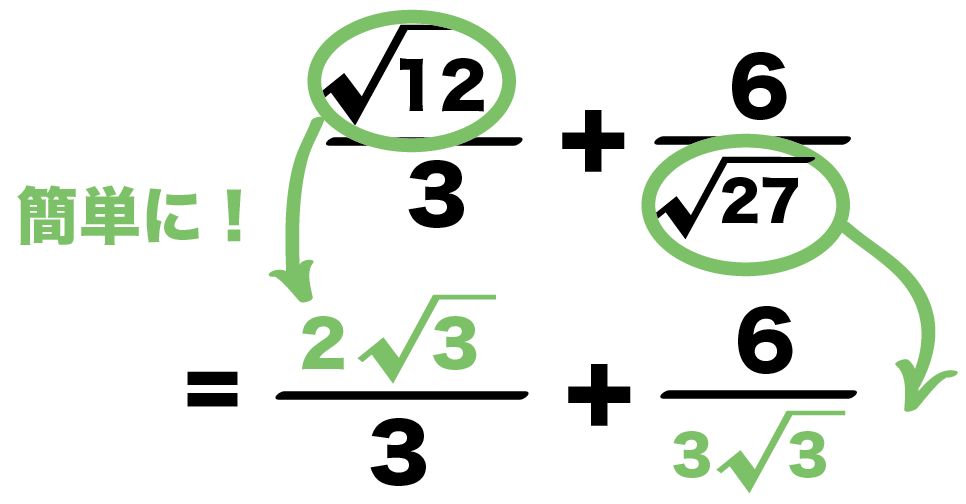
平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく

平方根 とは 根号の意味や性質 値の求め方について 数学fun

これで完璧 平方根の基礎 中3数学 家庭教師のlaf

日本ケイデンス デザイン システムズ The Sound Of Cadence Online

平方根 ルートとは 平方根の求め方を解説 分数や小数の場合はどうやる 数スタ

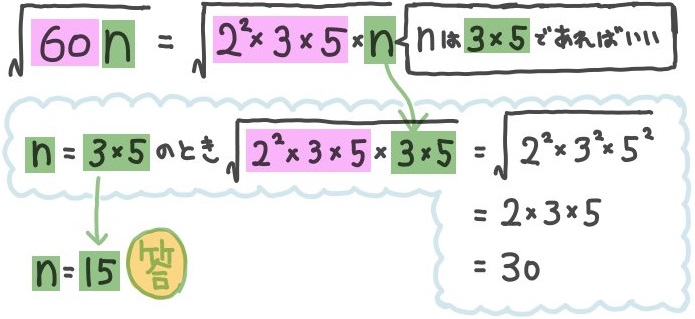
平方根の利用 ルートの中の自然数ｎを求める問題一覧 坂田先生のブログ

開平方 平方根の求め方 時じくの香の木の実

平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ

1

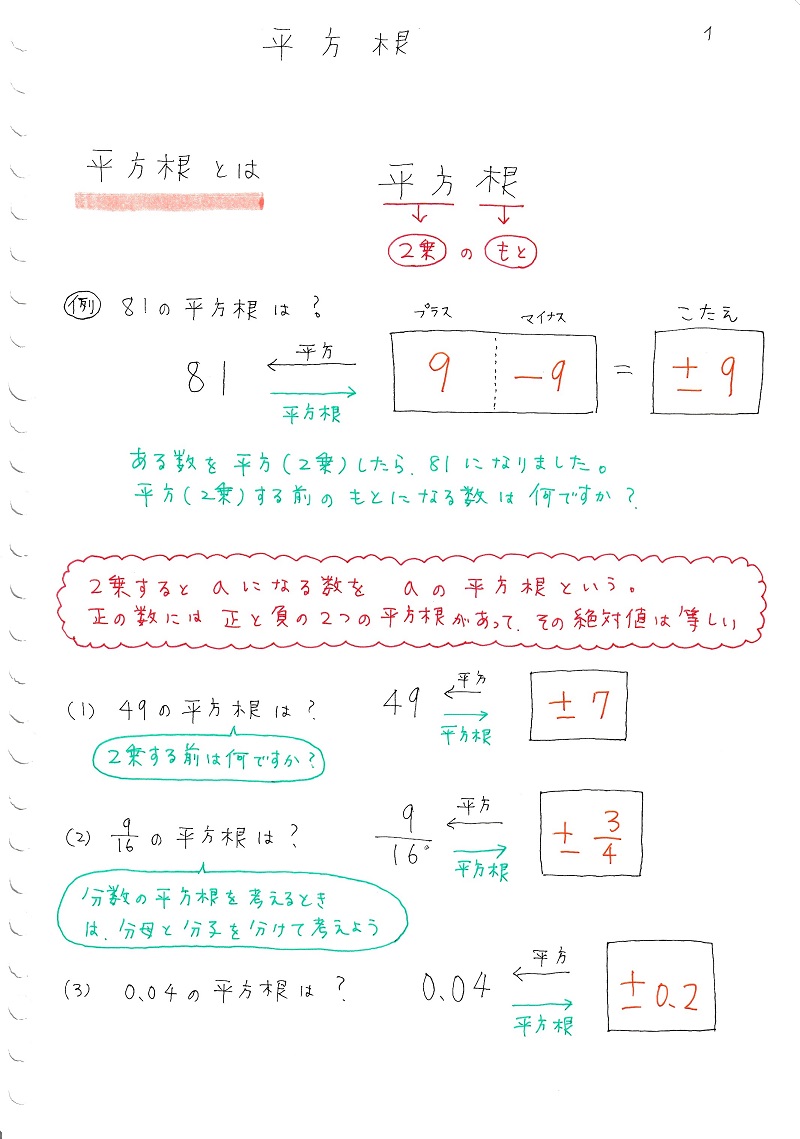
中学数学 平方根 ママ塾ノート

25の平方根は 5の平方根は Yahoo 知恵袋

平方根 超簡単にわかる 有理数と無理数 苦手な数学を簡単に

平方根の公式 中学生が覚えるべき掛け算と割り算の公式 中学や高校の数学の計算問題

なんで５の平方根がプラマイルート５なんですか そもそも何でプラマイ Yahoo 知恵袋

Ed2 City Yamato Kanagawa Jp

中学３年生 平方根の加減b 学童cafe チャイルドスペース

9の平方根は3と 3ということは分かるのですが どうして5の平方根はルート５ Clearnote

ルート足し算

楽天市場 平方根 人文 地歴 哲学 社会 本 雑誌 コミック の通販

５の平方根は ルート５ですか また ルートの中に５を入れると Yahoo 知恵袋

1 2乗って何 どうしてそれがルート 平方根 になるのか 数学の面白いこと 役に立つことをまとめたサイト

平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ

平方根の手計算による解法 タックの庭仕事 黄昏人生残日録

平方根とは すうがくのいえ

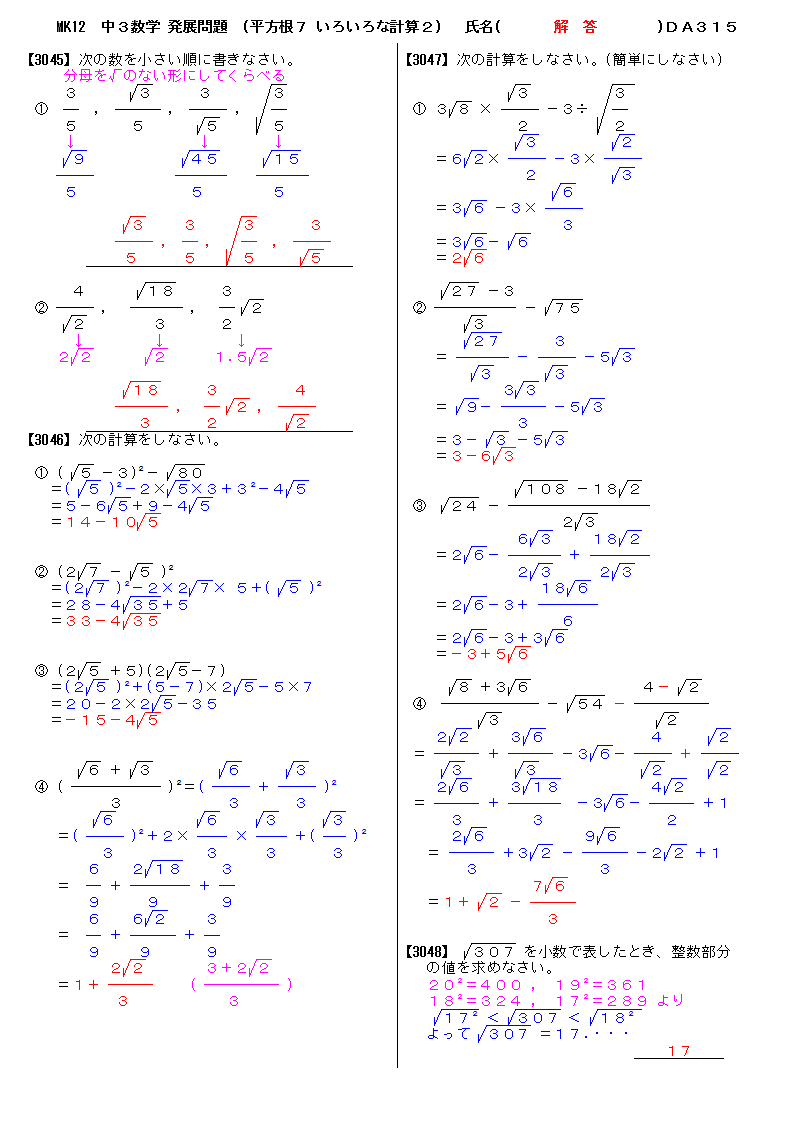
無料 中３数学 発展 応用問題 解答プリント 315 平方根７ いろいろな計算２

中３数学 平方根 ５の作図 Youtube

中３数学 平方根 ５ 中学数学高校数学個別指導in山形市 数専ゼミ

1 １ の は 5の平方根は 5 なのに なぜ2 の 2 Clearnote

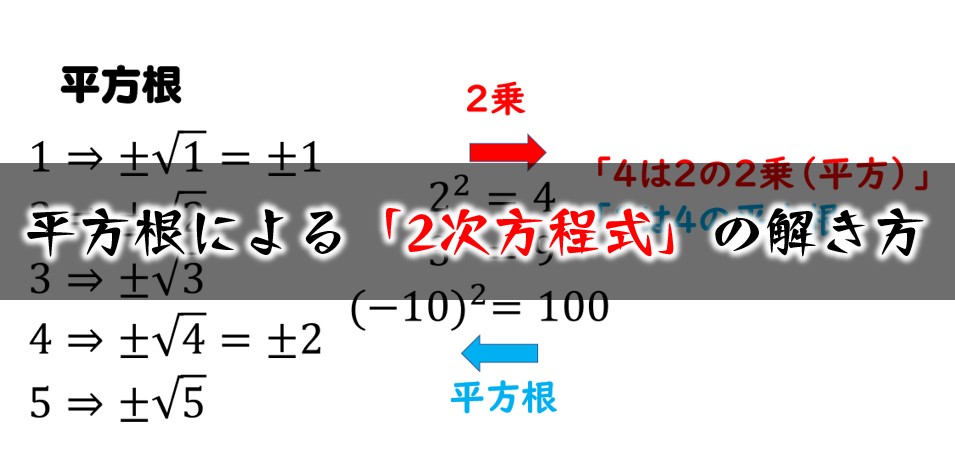
2次方程式の解き方 平方根を利用 数学fun

平方根 分母の有理化のやり方はこれでバッチリ 数スタ

Kouyama Sci U Toyama Ac Jp

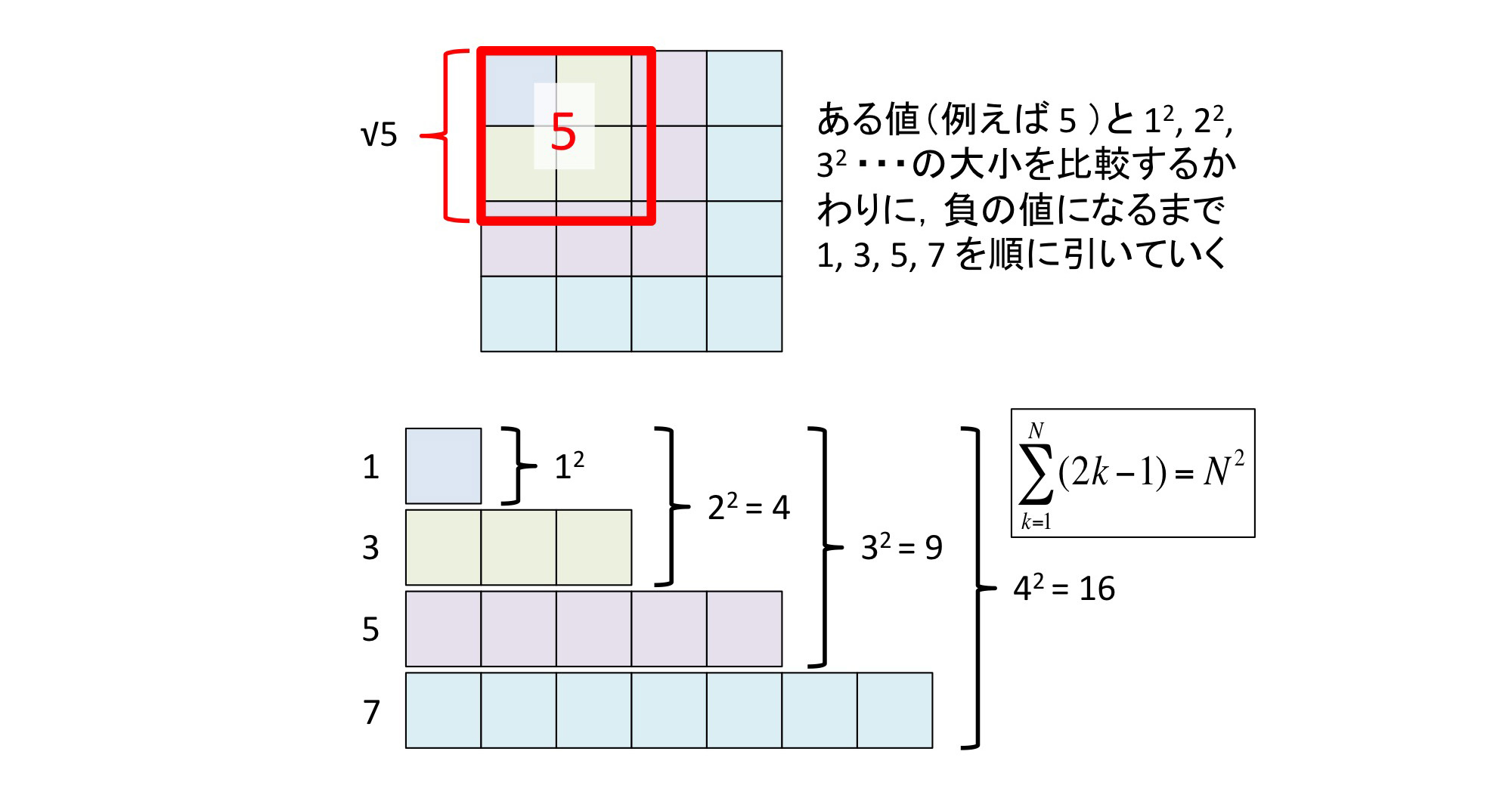
機械式計算機による平方根の計算

平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ

根号 の意味と覚え方 ルートは 何のために作られた 三重の個人契約家庭教師

中学３年数学 平方根 まとめテスト５ あんのん塾

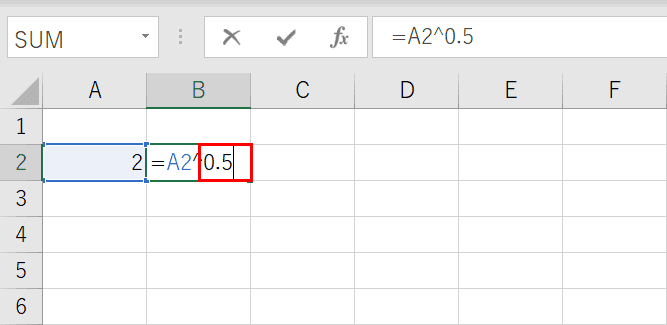
Excel関数 平方根 ルート を求める Sqrt関数

バカでもわかる 中学数学 平方根

Nhk Or Jp

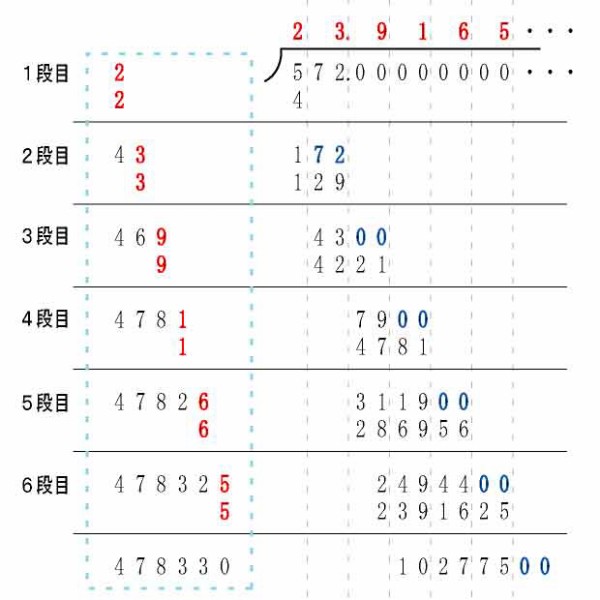
平方根の筆算のしかた

中学3年生数学 平方根の性質 長野地区 Itto個別指導学院 長野市の学習塾

平方根の問題の解き方 6パターン 数学fun

中学数学3年 平方根とその近似値 大小 有理数と無理数 受験の月

5の平方根ってないですよね 平方根の平方根ですか 余裕で Yahoo 知恵袋

平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ

無料 中３数学 発展 応用問題 問題プリント 314 平方根６ いろいろな計算１

Naka H Ibk Ed Jp

中３ 平方根５ 有理数と無理数 中学数学の勉強に